Working with MosFet’s
 The Metal-Oxide-Semiconductor Field-Effect Transistor, or MOSFET for short, is similar in many ways to the junction FET (JFET). Both are voltage-driven unipolar devices that depend on either electron or hole movement–but not both, as does the bipolar transistor. However, there is a fundamental structural difference between the two field-effect transistors: The JFET has three layers while the MOSFET has two. The MOSFET’s simpler construction has give it a performance edge over the JFET, and made it the world’s most popular transistor style.
The Metal-Oxide-Semiconductor Field-Effect Transistor, or MOSFET for short, is similar in many ways to the junction FET (JFET). Both are voltage-driven unipolar devices that depend on either electron or hole movement–but not both, as does the bipolar transistor. However, there is a fundamental structural difference between the two field-effect transistors: The JFET has three layers while the MOSFET has two. The MOSFET’s simpler construction has give it a performance edge over the JFET, and made it the world’s most popular transistor style.
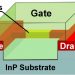
Earlier articles in this series stated that the MOSFET’s controlling gate voltage is applied directly to its channel region across a thin layer of insulating oxide, as shown in Fig. 1-a. This geometry contrasts with that of the JFET, which is controlled by switching an internal PN junction. The MOSFET will work from lower power that the JFET, and its simpler design is reflected in lower production costs. That is why it has become the basis for all CMOS digital logic IC families.
Part 9 and Part 11 in this series discussed FET’s. The basic principles of JFET’s and MOSFET’s were explained in the first article of (Electronics Now, February 1993) and the words that describe them were defined. The second article (Electronics Now, March 1993) focused on JFET’s, and included practical JFET circuit schematics.
This article concentrates on the enhancement-mode MOSFET, and it includes practical MOSFET circuit schematics base upon small-signal MOS transistors available in a low-cost CMOS integrated circuit. You might wish to review the first two articles to refresh your general knowledge of FET’s before reading this article.
MOSFET Basics:
There are both N- and P-channel MOSFET’s just as there are both N- and P-channel JFET’s. In the cross-section view of an N-type enhancement-mode transistor, Fig. 1a, you can see the thin layer of silicon dioxide (glass) that electrically isolates the metal gate from the channel between the N-doped source and drain regions. The presence of that insulated gate is why the MOSFET has also been called and IGFET (for insulated gate FET). However, that term is now considered obsolete.
 As shown in Fig. 1a, the channel between the N-type source and drain of an N-channel, enhancement-mode MOSFET is the substrate P-type material. This MOSFET can be turned on so that current flows between source and drain only when a positive forward bias is placed on the gate. As a result, the enhancement-mode MOSFET is said to be “normally off”. Its operation depends on the electron flow.
As shown in Fig. 1a, the channel between the N-type source and drain of an N-channel, enhancement-mode MOSFET is the substrate P-type material. This MOSFET can be turned on so that current flows between source and drain only when a positive forward bias is placed on the gate. As a result, the enhancement-mode MOSFET is said to be “normally off”. Its operation depends on the electron flow.
Recall, from Part 9’s article, that all JFET’s are depletion-mode or “normally on” devices. They are turned ‘off’ by applying reverse bias. Depletion-mode MOSFET’s are being made today for high-frequency radio applications.
A P-channel, enhancement-mode MOSFET has a cross section that is identical to that shown in Fig. 1-a except that the substrate is N-type material and the source and drain regions are P-type material. A negative forward bias is needed to turn a P-channel, enhancement-mode MOSFET ON. Its operation depends on the movement of holes, which have lower mobility than electrons. This means that an N-channel MOSFET can switch faster than a P-channel MOSFET.
As in the JFET, signal voltages or biases applied between the gate and source terminals of the MOSFET control the magnitudes of signal currents flowing between the drain and source terminals.


N- and P-channel MOSFET’s are said to be complementary because the doping of their substrate, source, and drain materials as well as their forward bias polarities are opposite.
However, as will be seen, advantage is taken of those characteristics in complementary MOS (CMOS) logic families and some of the circuit is discussed here.
Figure 1-b is the schematic symbol for an enhancement-mode N-channel MOSFET. The dotted vertical line between the drain and the source represents a “normally-off” channel. (The symbol for complementary P-channel device is similar except that its arrow points outwards.)
Figure 2-a shows a cross section of a monolithic CMOS IC with both N- and P-channel MOSFET’s integrated on the same substrate. The drains of both FET’S are connected. Fig. 1-b shows the schematic symbols for N- and P-channel MOSFET’s that are integrated into the CMOS chip shown in Fig. 1-a. A CMOS IC provides the small-signal transistors needed for the experiments described in this article.
In passing, it is worth stating that, although they are organized in a similar manner, the most advanced CMOS logic families have polysilicon rather than metal electrodes. Polysilicon, a pure form of silicon, is a conductor.
Figure 3 shows typical drain-to-source output characteristic curves for an N-channel, enhancement-mode MOSFET. Drain current (ID) increases with increases in positive gate-to-source bias.
These curves were obtained from a MOSFET transistor within a CMOS circuit that will be discussed in detail later. The characteristic curves of a P-channel MOSFET are similar except that drain current increases as its bias becomes more negative.
Figure 4 illustrates the gate-to-source transfer characteristics for the same enhancement-mode, N-channel MOSFET shown in Fig. 3. It shows how drain current (ID) increases directly (and almost linearly) with positive gate-to-source voltage (VGS), while the DC supply voltage (VDD) remains constant at 15 volts. Note that no significant drain current flows until the gate voltage rises to a threshold (VTH) value of a few volts. (This can also be seen if Fig. 3).
 Before proceeding with this discussion of MOSFET’s, it is important to point out that protective precautions must be taken when handling all MOSFET devices. All MOSFET’s are susceptible to damage from the discharge of electrostatic energy between any two pins.
Before proceeding with this discussion of MOSFET’s, it is important to point out that protective precautions must be taken when handling all MOSFET devices. All MOSFET’s are susceptible to damage from the discharge of electrostatic energy between any two pins.
Th extremely high input impedance of these devices lends itself readily to the buildup of electrostatic charges. Because the oxide that insulates the gate of a MOSFET typically breaks down with the application of about 80 volts, damage or destruction of the devices can be caused by higher levels of ElectroStatic Discharge (ESD).
Protective circuitry has been built into many discrete MOSFET’s and protective networks are now included in most (if not all) current manufactured CMOS IC’s. However, the high electrostatic charge generated simply by scuffing your shoes on a carpet and then touching the pins of a “protected” device can overwhelm those defenses and damage or destroy the part.
Ideally, all MOSFET parts handling should be done only at a workstation organized to protect against ESD. In the event that is it is not practical, at the very least a grounded wrist strap should be worn, and all CMOS parts handling should be done on a grounded conductive work surface.
Complementary Pair:
A small-scale, industry-standard CMOS IC that contains a number of accessible N- and P-channel enhancement-mode transistors is an excellent source of MOSFET’s for experiments. Figure 5 shows the schematic of a CD4007UB, a dual complementary pair plus inverter. It has six accessible MOSFET transistors: two pairs are unconnected and the third pair is connected as a CMOS inverter or NOT gate.


There are many sources for the CD4007UB, know generically as the 4007. Prefixes identify the manufacturer. The CD4007UB, for example, is made by Harris Semiconductor: it is pin-for-pin compatible with the Motorola MC14007UB.
These versatile parts are useful as digital logic parts as well as for linear applications in amplifiers, pulse-shapers, and crystal oscillators.
The suffix “UB” indicates a CMOS series whose gates and inverters are constructed with a single inverting stage between input and output, which results in decreased gain. However, this characteristic is useful when these normally digital logic products are operated in the “linear” regions of their characteristic curves.
Figure 5 is the schematic for the 4007UB in a 14-pin DIP package. The MOSFET’s have been labeled Q1 to Q6. Transistors Q1, Q3, and Q5 are P-channel devices, while Q2, Q4, and Q6 are N-channel devices. Pin access is given to all three terminals of transistors Q1 to Q4, but transistors Q5 and Q6 are permanently configures as an inverter.
The typical output and transfer characteristics of Figs. 3 and 4 were obtained from an N-channel MOS transistor Q2 of a 4007UB.
Figure 6 is the pin assignment diagram for the 4007UB. It has been supplemented with labels that relate pin numbers to the function they perform in the schematic. Fig. 5. Table-1 presents the outstanding characteristics of the 4007UB.
Figure 7 shows the protection network for the CD4007UB. Input diode D2 is a distributed resistor-diode network that appears as two diodes to (VDD)
 Application Rules:
Application Rules:
Here are some simple rules to keep in mind when working with the 4007UB:
- In any application, all unused elements of the device must be disabled.
Complementary pairs of MOSFET’s can be disabled by connecting them as standard
CMOS inverters, as shown in Fig. 8 (gate-to-gate and source-to-source), and
grounding their inputs. Refer to Fig. 5 to interpret the pin numbers given in
the figure. (The triangle symbol used here to designate a complementary pair of
transistors is the digital logic symbol for an inverter.) - Individual MOSFET’s can be disabled by connecting their sources to their
substrates and leaving their drains open-circuited. - Input terminals must not be allowed to rise above the supply voltage
(VDD) or fall below zero volts (VSS). - To use an N-channel MOSFET, the source must be tied directly to (VSS) or
through current-limiting resistor. Similarly, to use a P-channel MOSFET, the
source must be tied directly to (VDD) or through a
current-limiting resistor.

 Linear Operation:
Linear Operation:
Figure 9 shows how to connect Q2, an N-channel MOSFET in the 4007UB as a linear inverting (common-source) amplifier. Resistor R1 is the drain load of Q2, and series resistors R2 and (RX) form a voltage divider that biases the gate so that Q2 operates in the linear region.
The value of (RX) is selected to give the desired quiescent drain voltage. It is normally in the range 18,000 to 100,000 ohms.
Figure 10 shows how the Fig. 9 circuit is modified to give it very high input impedance. The 10-megoHm isolating resistor R3 is placed between the function of resistors R2 and (RX) and the gate of Q2.
Figure 11 show how to connect Q2 as a unity-gain, non-inverting (common-drain) amplifier or source-follower. If the gate of Q2 is biased at half-supply voltage by the voltage divider made up of R2 and R3, the source pin assumes a quiescent value that is slightly more than the threshold voltage VTH below the gate value. The circuit has an input impedance equal to the values of resistors R2 and R3 in parallel (50,000), but this value can easily be increased to greater than 10 megohms by inserting resistor R4 as shown in the figure.
Alternatively, the input impedance of the circuit in Fig. 11 can be raised to several hundred megoHms with the “bootstrapped” source-follower configuration shown in fig. 12. The output signal from Q2 is fed back to the junction through capacitor C1. As a result, near-identical input signals appear at each end of resistor R4, which, in turn, passes near-zero signal current and appears (to the input signal) as a near-infinite impedance.
It can be seen from the previous descriptions that an enhancement-mode MOSFET acts like a bipolar transistor, except that:
- It exhibits very high input impedance.
- It has a self-limiting drain-to-source current.
- It has a substantially larger input-off-set voltage than a bipolar transistor.
The base-to-emitter offset of a bipolar transistor is typically 600 millivolts, while the gate-to-source offset of a MOSFET is typically 2 volts. If one allows for those differences, a small-signal, enhancement-mode MOSFET can replace a small-signal bipolar transistor in many kinds of bipolar transistor circuits.



The CMOS Inverter:
The most basic CMOS circuit is a complementary pair of N- and P-channel MOSFET’s connected in series to form an inverter. The inverter shown in Fig. 13-a was specifically intended for digital circuitry where it performs the NOT operation. Fig. 2 is a section view of N- and P-channel MOSFET’s integrated on the same chip with a common drain connection. This device can be converted to the CMOS inverter shown in Fig. 13-a by connecting the gates of P-channel MOSFET Q1 and N-channel MOSFET Q2 to form input terminal VIN, and taking the output VOUT from the common drain. The source of Q1 is connected to the positive power supply VDD, and the source of Q2 is grounded at VSS.Consider the P-channel MOSFET Q1 to be the driver and the N-channel MOSFET Q2 to be the load. Recall that an N-channel MOSFET conducts with a positive gate bias, and a P-channel enhancement-mode MOSFET conducts with a negative gate bias.
When the voltage at the input terminal VIN is low (logic zero), the voltage on the gate of Q1 is negative, causing it to conduct and short the supply voltage VDD to the output terminal VOUT because Q2 is OFF (its gate voltage zero), a high-impedance path exists between VOUT to ground VSS. As a result the voltage at VOUT is VDD.
Alternately, when the input voltage is high (logic 1), the situation is reversed: Q1 is cut OFF, forming a high-impedance path between VDD and VOUTS and Q2 conducts, forming a low-impedance path from VOUT to ground VSS, causing the output voltage to fall to zero.
 This response makes the circuit a logic inverter or NOT gate. As can be seen in the truth table, Fig. 13-b, a low (logic 0) input results in a high (logic 1) output; conversely, a high (logic 1) input results in a low (logic 0) output.
This response makes the circuit a logic inverter or NOT gate. As can be seen in the truth table, Fig. 13-b, a low (logic 0) input results in a high (logic 1) output; conversely, a high (logic 1) input results in a low (logic 0) output.In either logic state one enhancement-mode MOSFET is ON while the other is OFF. Because of this, the quiescent current of a CMOS inverter is extremely low. It is this quality that gives the CMOS digital logic IC families their many advantages.
Figure 13-c is the accepted logic symbol for a NOT gate. (This symbol was used in Fig. 8 to simplify the discussion of disabling unused complementary pairs).
Although the CMOS digital inverter consumes zero quiescent current, it can source (feed) or sink (absorb) significant current into or out from external loads. When the input is at logic-0, the output is effectively shorted by Q1 to the positive power supply, so substantial current can feed through Q1 into a load connected to its output.
When the input to the digital inverter is at logic-1, the output is effectively shorted by Q2 to ground, so significant current can be drawn through Q2 from a load connected between the output and the positive supply. This is another very important feature of the CMOS digital inverter circuit.


A CMOS inverter can become a linear inverting amplifier by biasing its input terminal VIN at a value intermediate between the logic-0 and logic-1 levels. In this situation Q1 and Q2 are both partly biased ON, so the inverter passes significant quiescent current.
Figure 14 shows the typical drain-current transfer characteristics of the linear inverting amplifier under this intermediate condition. Drain current (ID) is effectively zero when the input voltage (VIN) is either at zero or full supply volts. However, drain current rises to its maximum value when the input voltage is approximately half the supply voltage.
Three different supply voltage (VDD) conditions are shown in Fig. 14: 5, 10, and 15 volts. These result in drain currents of 0.5 milliamperes, 4 milliamperes, and 10.5 milliamperes, respectively. Under these conditions both inverter MOSFET’s are biased ON equally.Figure 15 shows typical input-to-output voltage-transfer characteristic’s for a CMOS inverter at three different power supply voltage VDD values: 15, 10, and 5 volts. With a 15-volt supply, for example, the output voltage changes only a small amount when the input voltage is shifted between the VDD and zero-volt levels.
 However, when VIN is biased a roughly half the supply voltage, a small change of input voltage causes a large change of output voltage. In the half-supply condition, the inverter typically provides a voltage gain of about 30 dB when used with a 15-volt supply, or 40 dB with a 5-volt supply.
However, when VIN is biased a roughly half the supply voltage, a small change of input voltage causes a large change of output voltage. In the half-supply condition, the inverter typically provides a voltage gain of about 30 dB when used with a 15-volt supply, or 40 dB with a 5-volt supply.Figure 16 shows a CMOS inverting amplifier. This circuit is biased automatically by connecting a 10-megohm resistor R1 between the input and output terminals. As a result, the output self-biases at approximately half the supply voltage.
 Figure 17 shows typical voltage gain and frequency characteristic curves for a CMOS inverter stage when it is powered at three different levels: 15, 10, and 5 volts. These curves were obtained when the amplifier output fed into the high impedance of a 10-megohm, 15-picoFarad oscilloscope probe. Under this condition, the circuit has a bandwidth of 2.5 MHz when operated from a 15-volt supply.
Figure 17 shows typical voltage gain and frequency characteristic curves for a CMOS inverter stage when it is powered at three different levels: 15, 10, and 5 volts. These curves were obtained when the amplifier output fed into the high impedance of a 10-megohm, 15-picoFarad oscilloscope probe. Under this condition, the circuit has a bandwidth of 2.5 MHz when operated from a 15-volt supply.As might be expected from the voltage transfer curves in Fig. 15, the distortion characteristics of the CMOS linear amplifier are not very good. The linearity is acceptable with small-amplitude signals whose output amplitudes reach 3 volts peak-to-peak with a 15-volt supply. However, distortion increases progressively as the output approaches the upper and lower power supply limits. Unlike a bipolar transistor circuit, the CMOS amplifier does not “clip” excessive sinewave signals; it progressively rounds off their peaks.
Figure 18 shows the typical drain-current vs. supply-voltage characteristics of the CMOS linear amplifier. The drain current (ID) typically swings from 0.5 milliampere at 5 volts (VDD) to 12.5 milliamperes at 15 volts (VDD).
In many applications the quiescent supply current of the 4007UB CMOS amplifier can be reduced with a penalty of reduced amplifier bandwidth by placing external resistors in series with the source terminals of the two MOSFET’s of the CMOS stage. This is illustrated as the micropower circuit of Fig. 19.
 Table 2 shows the measured results of placing different values of resistor in the source circuits of transistors Q5 and Q6.
Table 2 shows the measured results of placing different values of resistor in the source circuits of transistors Q5 and Q6.
With changing values of both R1 and R2, a constant supply voltage (VDD of 15 volts, and the output loaded by a 10-megohm, 15-picofarad oscilloscope probe, the results can be read across the table. They are drain current (ID), voltage gain, and upper 3dB bandwidth.The additional resistors shown in the circuit of Fig. 19 increase the output impedance of the amplifier. (The output impedance is roughly equal to the R1-voltage gain product.) This impedance and the external load resistance and capacitance has a significant effect on the overall gain and bandwidth of the circuit.
When the values of R1 and R2 are 10,000 ohms, it can be seen that if the load capacitance is increased from 15-picofarads to 50 picofards, the bandwith fall to abot 4 kHz. However, if th ecapacitance is reduced to 5 picofarads, the bandwidth is increased to 45 kHz. Similarly, if the resistive load is reduced from 10 megohms to 10,000 ohms, th evoltage gain falls to unity. thus, to obtain significant gain, the load resistance must be large relative to the output impedance of the amplifier.
The basic (unbiased) CMOS inverter stage has an input capacitance of about 5 picofarads and an input resistance of near infinity. Thus, if the output of the circuit in fig. 19 is fed directly to such load, it will show a voltage gain of about 30 and a bandwidth of 3 kHz when R1 and R2 are both 1 megohm. The amplifier will work when R1/R2 value is 10 megohm, but it will consume a quiescent current of only 0.4 microampere.


 Practical CMOS Circuits:
Practical CMOS Circuits:
A CMOS linear amplifier will function in either its standard or micropower forms ot provided a wide range of fixed-gain amplifiers, mixers, integrators, active filters, and oscillators. Figures 20 to 24 are examples of some of the possible circuits derived from the amplifier. Figure 20 shows the practical circuitof a X10 inverting amplifier. The CMOS stage is biased by feedback resistor R2, and the voltage gain is set at X10 by the ratio of resistor R2 to resistor R1. The input impedance of the circuit is 1 megohm, and that equals the value of resistor R1.
Figure 20 shows the practical circuitof a X10 inverting amplifier. The CMOS stage is biased by feedback resistor R2, and the voltage gain is set at X10 by the ratio of resistor R2 to resistor R1. The input impedance of the circuit is 1 megohm, and that equals the value of resistor R1.Figure 21 shows how the circuit in fig. 20 can be modified to become an audio mixer or analog voltage adder. The circuit has four input pins, and the voltage gain between each input and the output pin is held at unity by the relative values of the 1-megohm feedback resistor. Figure 22 shows how the basic CMOS amplifier is organized as a simple integrator.
 Figure 23 shows how a linear CMOS amplifier can function as a crystal oscillator. The CMOS amplifier is biased into the linear region by resistor R1, which provides a 180° phase shift. The pi-type crystal network formed by Rx, C1 and C2, and XTAL1, provides the additional 180° of phase shift at the resonant frequency to cause the circuit to oscillate.
Figure 23 shows how a linear CMOS amplifier can function as a crystal oscillator. The CMOS amplifier is biased into the linear region by resistor R1, which provides a 180° phase shift. The pi-type crystal network formed by Rx, C1 and C2, and XTAL1, provides the additional 180° of phase shift at the resonant frequency to cause the circuit to oscillate. If you only want the circuit to oscilate at a frequency accurate within about 0.1%, resistor Rx can be replaced with a shorting wire and both capacitors C1 and C2 can be omitted. For ultra-high accuracy, however, the correct values of Rx, C1, and C2 must be individually determined.
If you only want the circuit to oscilate at a frequency accurate within about 0.1%, resistor Rx can be replaced with a shorting wire and both capacitors C1 and C2 can be omitted. For ultra-high accuracy, however, the correct values of Rx, C1, and C2 must be individually determined. Figure 24 shows the schematic for a micropower version of the CMOS crystal oscillator. In this circuit, Rx is included in the amplifier. The output of this oscillator can be fed directly to the input of another CMOS inverter stage if you want a more precise waveform shape and higher amplitude.
Figure 24 shows the schematic for a micropower version of the CMOS crystal oscillator. In this circuit, Rx is included in the amplifier. The output of this oscillator can be fed directly to the input of another CMOS inverter stage if you want a more precise waveform shape and higher amplitude.